Answer:
262ft
Explanations:
From the given information, we have the following data:
• Height of the pole = 10ft
,
• Length of the tower's shadow = 177ft
,
• Length of the pole shadow = 6.75ft
Required
• Height of the tower (H)
To get the height of the tower, you will use the similarity theorem of triangles as shown:

Substitute the given parameters into the formula to have:
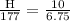
Cross multiply

Therefore, the height of the tower to the nearest foot is 262ft