For the surface area:
We have:
• Two triangles with base = 21 cm and height = 8 cm :
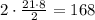
• A 21 cm x 30 cm rectangle:
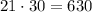
• A 17 cm x 30 cm rectangle:
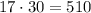
• A 10 cm x 30 cm rectangle:
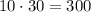
Adding up the surface area of all the faces, we'll get the total surface area of the prism:
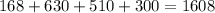
Thereby, the surface area of the prism is 1608 square centimiters
For the volume:
We can see the prism as a body with triangular base and a height of 30 cm. To calculate teh volume, we calculate the area of the base and multiply it by the height.
The base is a triangle with base = 21 cm and height = 8 cm :
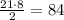
Multiply by the height to get the volume:
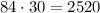
We get that the volume of the prism is 2520 cubic centimiters.