First, we must remember that if a sequence is geometric, that of finding the sum of the first n terms, called Sn, without having to add all the terms.
To do this, we use the following equation:
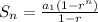
Where in this case we have:

Now, we replace these values and solve the sum:
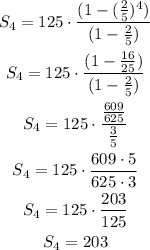
In conclusion, the sum of the geometric series with a1= 125, r=2/5, n=4 is a total of 203.