Question

Question will be in picture

Answer 1

Consider the standard form of a quadratic equation is,

`y=ax^2+bx+c`

It's vertex (h,k) is given by,

`\begin{gathered} h=(-b)/(2a) \\ k=f((-b)/(2a)) \end{gathered}`

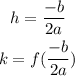
Now consider the given equation,

`y=x^2-2x+4`

So its vertex will be,

`\begin{gathered} h=(-(-2))/(2(1))=1 \\ k=(1)^2-2(1)+4=1-2+4=3 \end{gathered}`

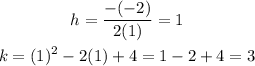
So the vertex of the quadratic equation lies at (1,3).

Now, observe the given graphs.

It is found that only first graph shows the vertex at point (1,3).

So option a will be the correct choice.