Consider the standard form of a quadratic equation is,
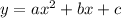
It's vertex (h,k) is given by,
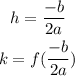
Now consider the given equation,
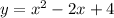
So its vertex will be,
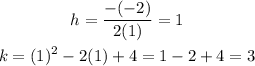
So the vertex of the quadratic equation lies at (1,3).
Now, observe the given graphs.
It is found that only first graph shows the vertex at point (1,3).
So option a will be the correct choice.