Question

a population of a school is 800 and is decreasing at a rate of 2% per year. Write an exponential decay function to model the given situation. Then find the population after 4 years

Answer 1

Exponential Decay Function

An exponential decaying function is expressed as:

`C(t)=C_o\cdot(1-r)^t`

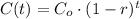
Where:

C(t) is the actual value of the function at time t

Co is the initial value of C at t=0

r is the decaying rate, expressed in decimal

We are given the initial population of a school Po=800. We also know the rate of change is r=2%=0.02 per year.

Substituting the values in the exponential model, using the variable P for the population:

`P(t)=800\cdot(1-0.02)^t`

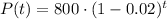
Calculating:

`P(t)=800\cdot(0.98)^t`

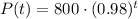
This is the required equation for the model.

The population after t=4 years is:

`P(4)=800\cdot(0.98)^4`

Using a scientific calculator:

`\begin{gathered} P(4)=800\cdot0.9224 \\ P(4)\approx738 \end{gathered}`

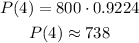
The population after 4 years will be approximately 738