Question

the equation, ^2/16 − ^2/4 = 1, the vertices of the hyperbola are located at points a. (±16,0)b. (±4,2) c. (±4,0)d. (±2,0)e.(±2√5, 0)

Answer 1

The hyperbola is given by the equation

`(x^2)/(16)-(y^2)/(4)=1`

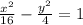
Notice that this is a hyperbola centered in the origin. Furthermore, as the x^2 is positive and the y^2 is negative, we can know that the graph opens to the right and the left; therefore, we expect the lines that cross the vertices of the hyperbola to be in a line of the form:

`x=k;k\text{ a constant}`

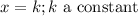
To sum up, given the characteristics of the equation, the hyperbola looks like this:

We need to find the value of the blue lines. For this, set y=0 and solve the equation as follows:

`\begin{gathered} y=0 \\ \Rightarrow(x^2)/(16)=1 \\ \Rightarrow x^2=16 \\ \Rightarrow x=\pm4 \end{gathered}`

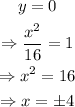
Therefore, the vertices are (4,0) and (-4,0). Option C is the answer