Given that
There is a square pyramid with its height, h = 12 units and base edge, a = 10 units
And we have to find the surface area of the pyramid.
Explanation -
The surface area of the square pyramid is given as
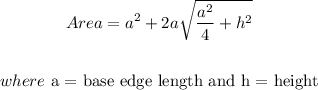
On substituting the values we have
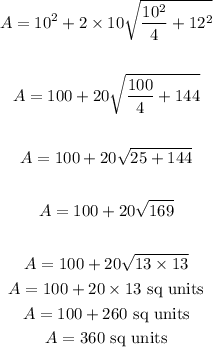
So the required area is 360 sq units and OPTION B is correct.
Final answer -
Therefore the final answer is 360.