Answer:
D. The number could be 1,2,3,4,5,6 or 7.
Step-by-step explanation:
Let the number = n
Twice the number = 2n
Five more than twice a number = 2n+5
If the expression above is less than 20, we have:
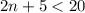
We solve for n.
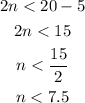
Since n is less than 7.5, the number could be 1,2,3,4,5,6 or 7.