Answer:
• Discriminant =0
,
• Number of Solutions = One repeated root
Step-by-step explanation:
Given the quadratic equation below:
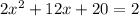
First, we express it in the general form of a quadratic equation: ax²+bx+c=0
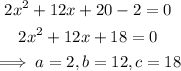
Next, we find the discriminant.
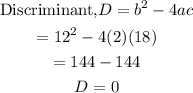
Since the discriminant equals 0.
The quadratic equation has One Repeated Root.