So,
Let "x" be the amount that we want to find.
We know that 15% of x equals 22.5. We could write this as the following equation:
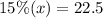
15% is the same to write 15/100. So,
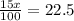
Now, let's solve this equation for x:
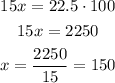
We can represent a percentage always dividing the number by 100:
For example,

In this problem, we need to represent 15%, so that's 15/100. The only thing we did until then, was to rewrite the percentage. Then, just state the equation:
If 15% of x = 22.5, we should find x, so, we multiply by cross and obtain that x=150.