Question

Find the equation of the line tangent to the curve y=3sinx +2Cosx at x=0

Answer 1

Given that the equation of the curve is

`y=3\sin x+2\cos x`

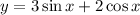
at x=0.

Differentiate y with respect to x to find the slope of the tangent line.

`(dy)/(dx)=3(d(\sin x))/(dx)+2(d(\cos x))/(dx)`

`(dy)/(dx)=3\cos x-2\sin x`

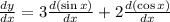
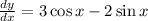
Substitute x=0, we get

`(dy)/(dx)=3\cos (0)-2\sin (0)`
`(du)/(dx)=3`

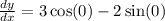
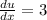
We get slope =3.

Substitute x=0 in y, we get

`y=3\sin (0)+2\cos (0)`

`y=2`

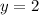
We get the point (0,2).

Recall the formula for the point-slope

`y-y_1=m(x-x_1)`
`\text{ Substitute }x_1=0.y_1=2,\text{ and m=3, we get}`

`y-2_{}=3(x-0_{})`

`y-2_{}=3x`

`y_{}=3x+2`

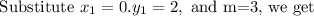
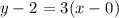
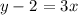
Hence the equation of the line tangent to the curve y=3sinx +2Cosx at x=0 is

`y_{}=3x+2`