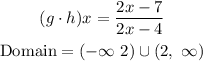Question

Composition of two functions: AdvancedFor the real-valued functions g(x) =*** and h(x) = 2x-5, find the composition g h and specify its domain using interval notation.

Answer 1

As per given by the question,

There are given that two function,

`\begin{gathered} g(x)=(x-2)/(x+1) \\ h(x)=2x-5 \end{gathered}`

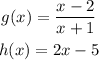
Now,

For find the value of (g.h)x,

Put the value of h(x) into the g(x).

So,

From the given function;

`(g\cdot h)x=(x-2)/(x+1)\cdot2x-5`

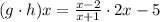
Then,

Put the value of h(x) into g(x) instead of x.

So,

`(g\cdot h)x=(2x-5-2)/(2x-5+1)`

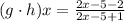
Now, solve the above function.

`\begin{gathered} (g\cdot h)x=(2x-5-2)/(2x-5+1) \\ (g\cdot h)x=(2x-7)/(2x-4) \end{gathered}`

Now,

Domain of the above function,

From the fuction;

`(g\cdot h)x=(2x-7)/(2x-4)`

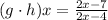
For the domain of the given function ,

Set the denominator in equal to 0.

Then,

`\begin{gathered} 2x-4=0 \\ 2x=4 \\ x=2 \end{gathered}`

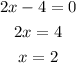
The domain is all values of x that make the expression defined in interval notation is;

`(-\infty\text{ 2)}\cup(2,\text{ }\infty)`

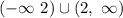
Hence, the value of (g.h)x and their domain is given below;

`\begin{gathered} (g\cdot h)x=(2x-7)/(2x-4) \\ \text{Domain}=(-\infty\text{ 2)}\cup(2,\text{ }\infty) \end{gathered}`