Let's start by making a sketch:
To figure out the perimeter, we will need all sides.
Since this is a right triangle, we can use trigonometric ratios to find them.
We know the leg adjacent to the 30° angle, so we can use tangent of 30° to find the other leg and either cosine or sine of 30° to find the hypotenuse afterwards.
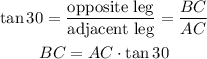
Tanget of 30° degree is known to be:
![\tan 30\degree=\frac{\sqrt[]{3}}{3}](https://img.qammunity.org/2023/formulas/mathematics/college/7037r8cqfb5e9nkzc8s83c0r8uqt9hj8gh.png)
So:
![BC=AC\cdot\tan 30\degree=7\sqrt[]{2}\cdot\frac{\sqrt[]{3}}{3}=\frac{7\sqrt[]{6}}{3}](https://img.qammunity.org/2023/formulas/mathematics/college/zkb265o8jylbyrr3eotzcnelp13rdr21ls.png)
And the value for cosine of 30° is also known:
![\cos 30\degree=\frac{\sqrt[]{3}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/1lsbvxvzhex3epev9f9a80im06r4yhyo8p.png)
So:
![\begin{gathered} \cos 30\degree=\frac{\text{adjacent leg}}{\text{hypotenuse}}=(AC)/(AB) \\ AB=(AC)/(\cos30\degree)=\frac{7\sqrt[]{2}}{\frac{\sqrt[]{3}}{2}}=\frac{14\sqrt[]{2}}{\sqrt[]{3}}=\frac{14\sqrt[]{2}\sqrt[]{3}}{3}=\frac{14\sqrt[]{6}}{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/gpv0zd9u6seyxjzmgsalt90gkjugoehwlo.png)
So, the perimeter will be:
![\begin{gathered} P=AB+BC+AC \\ P=\frac{14\sqrt[]{6}}{3}+\frac{7\sqrt[]{6}}{3}+7\sqrt[]{2} \\ P=\frac{21\sqrt[]{6}}{3}+7\sqrt[]{2} \\ P=7\sqrt[]{6}+7\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/mersyr19fkhp75sdfq64el81ydpdtaro9y.png)
Which corresponds to the third alternative.