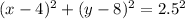Solution
- The diameter of a circle is the longest chord of a circle.
- Thus, the coordinate of the center of the circle is the midpoint of the diameter or longest chord.
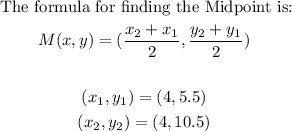
- Thus, we can solve the question as follows:
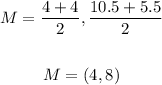
The center of the circle is (4, 8)
- The radius can be gotten by finding the distance between the coordinate of the center and any of the endpoints of the diameter.
- Thus, we have:
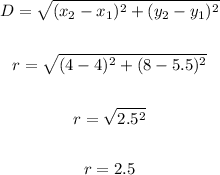
- The radius has a magnitude of 2.5 units
- The equation of the circle can be gotten by the formula given below:

The equation of the circle becomes: