the standard form of the quadratic function that meets the given conditions is:
![\[ y = x^2 - 8x + 21 \]](https://img.qammunity.org/2023/formulas/mathematics/college/xw5i8mz2x7ha2946f2a67co8nj0fc3abgq.png)
Therefore, the answer is option B.
To find the standard form of the quadratic function
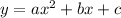 that has a vertex at
that has a vertex at
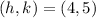 and passes through the point
and passes through the point
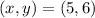 , we can use the vertex form of a quadratic function and then convert it to standard form. The vertex form of a quadratic function is:
, we can use the vertex form of a quadratic function and then convert it to standard form. The vertex form of a quadratic function is:
![\[ y = a(x - h)^2 + k \]](https://img.qammunity.org/2023/formulas/mathematics/college/jrpvmja33fdphhec9v1yiuwtdixj4oq48b.png)
Given the vertex
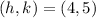 , we have:
, we have:
![\[ y = a(x - 4)^2 + 5 \]](https://img.qammunity.org/2023/formulas/mathematics/college/vavvzsg949f5ts5lmonrw5qfwwtb1p2nbd.png)
Now we need to determine the value of \(a\) using the point \((5, 6)\):
![\[ 6 = a(5 - 4)^2 + 5 \]](https://img.qammunity.org/2023/formulas/mathematics/college/tz3seo0gt7000e1vvfaxrpic535uvmtc00.png)
![\[ 6 = a(1)^2 + 5 \]](https://img.qammunity.org/2023/formulas/mathematics/college/p1lzmo9slool7h0b22l7h1950vsizihlh0.png)
![\[ a = 6 - 5 \]](https://img.qammunity.org/2023/formulas/mathematics/college/9k5ck5geguv1rn0bhht6jpgymvbxm3iz8r.png)
![\[ a = 1 \]](https://img.qammunity.org/2023/formulas/mathematics/college/a56yoxp3vk7uq886xcpoua9mbenvr1rszz.png)
So the equation in vertex form is:
![\[ y = (x - 4)^2 + 5 \]](https://img.qammunity.org/2023/formulas/mathematics/college/jq9omov57e1j9kpeqjs6o3fidestwpl3qi.png)
To convert this to standard form, we expand the squared term:
![\[ y = (x^2 - 8x + 16) + 5 \]](https://img.qammunity.org/2023/formulas/mathematics/college/c7gflf71asi2ig2fvpyw2me3xa4kyxyzhx.png)
![\[ y = x^2 - 8x + 21 \]](https://img.qammunity.org/2023/formulas/mathematics/college/xw5i8mz2x7ha2946f2a67co8nj0fc3abgq.png)
Thus, the standard form of the quadratic function that meets the given conditions is:
![\[ y = x^2 - 8x + 21 \]](https://img.qammunity.org/2023/formulas/mathematics/college/xw5i8mz2x7ha2946f2a67co8nj0fc3abgq.png)
Therefore, the answer is option B.