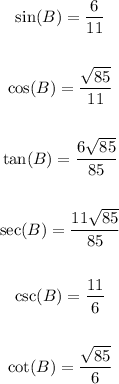Question

Find the exact values of the five remaining trig functions for B if sin(B) = 6/11.

Answer 1

First, recall the definition of the remaining trigonometric functions in terms of sin(x) and cos(x):

`\begin{gathered} \tan(x)=(\sin(x))/(\cos(x)) \\ \\ \sec(x)=(1)/(\cos(x)) \\ \\ \csc(x)=(1)/(\sin(x))} \\ \\ \cot(x)=(\cos(x))/(\sin(x)) \end{gathered}`

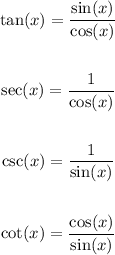
On te other hand, recall the Pythagorean Identity:

`\sin^2(x)+\cos^2(x)=1`

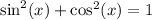
We can obtain an expression for cos(x) in terms of sin(x) using the Pythagorean Identity as follows:

`\cos(x)=√(1-\sin^2(x))`

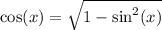
Find cos(B) using the expression for cosine in terms of sine. Then, use the values of cos(B) andsin(B) to find the values of tan(B), sec(B), csc(B) and cot(B):

`\begin{gathered} \sin(B)=(6)/(11) \\ \\ \cos(B)=\sqrt{1-\left((6)/(11)\right)^2}=\sqrt{1-(36)/(121)}=\sqrt{(121-36)/(121)}=(√(85))/(11) \end{gathered}`

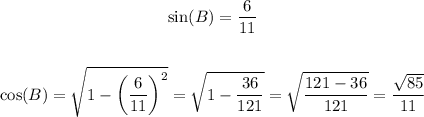
Then:

`\begin{gathered} \tan(B)=((6)/(11))/((√(85))/(11))=(6)/(√(85))=(6√(85))/(85) \\ \\ \sec(B)=(1)/((√(85))/(11))=(11)/(√(85))=(11√(85))/(85) \\ \\ \csc(B)=(1)/((6)/(11))=(11)/(6) \\ \\ \cot(B)=((√(85))/(11))/((6)/(11))=(√(85))/(6) \end{gathered}`

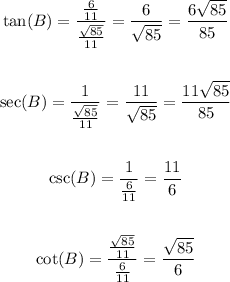
Therefore, the answers are:

`\begin{gathered} \sin(B)=(6)/(11) \\ \\ \cos(B)=(√(85))/(11) \\ \\ \tan(B)=(6√(85))/(85) \\ \\ \sec(B)=(11√(85))/(85) \\ \\ \csc(B)=(11)/(6) \\ \\ \cot(B)=(√(85))/(6) \end{gathered}`