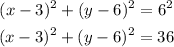Take into account that the general equation of a circumference is given by:

where (h,k) is the center of the circle and r the radius.
To determine the center of the circle calculate the coordinates of the midpoint between the endpoints of the diameters:
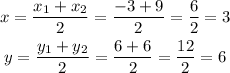
hence, the midpoint is (h,k) = (3,6) and it is the center of the circle.
To determine the radius of the circle, find first the lengh of the diameter, as follow:
![\begin{gathered} d=\sqrt[]{(-3-9)^2+(6-6)^2} \\ d=\sqrt[]{144}=12 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/vsm8bik1nluraxxg08cf8row58a813dfq9.png)
Then, the radius is:
r = d/2 = 12/2 = 6
By replacing the previous values of h, k and r into the general equation for a circle, you obtain: