The general form of a trigonometric function is:

Where B is the frequency of the function.
In our problem, A=1, C=D=0.
Then, as the value of B increases, so the frequency does. The answer to the second gap is 'increases'.
On the other hand, let P be the period and f the frequency. Those two quantities are related by the formula:
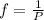
Then, if the frequency increases, the period decreases. The answer to the first gap is 'decreases'.
Finally, if B is negative we have that:
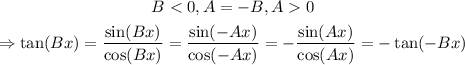
Therefore, the function is reflected over the x-axis.