Question

Hello! Need some help on parts a,b, &c. The question and rubric is linked below. Thank you!

Answer 1

Answer:

Part A: -5/9, 6/10, -7/11, 8/12

Part B:

`f(n)=(-1)^(n)((n)/(n+4))`

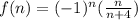
Part C: Positive

Step-by-step explanation:

The given sequence is:

`-(1)/(5),(2)/(6),-(3)/(7),(4)/(8),....`

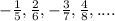
As seen above the sequence is an alternating sequence because it changes in sign

Also, neglecting the sign chnages, we will observe, a common diffference of 1 in the numerator and denominator

a) Therefore, if the pattern continues, the next 4 terms in the sequence are:

-5/9, 6/10, -7/11, 8/12

b)

Without the sign, the explicit equation representing the numerator is calculated below:

1, 2, 3, 4......

The first term, a = 1

The common difference, d = 1

This is an arithmetic sequence

N(n) = a + (n - 1)d

N(n) = 1 + (n - 1)(1)

N(n) = 1 + n - 1

N(n) = n

The explicit equation representing the denominator is calculated below

5, 6, 7, 8........

The first term, a = 5

The common difference, d = 1

D(n) = a + (n - 1)d

D(n) = 5 + (n - 1)(1)

D(n) = 5 + n - 1

D(n) = n + 4

The alternating sequence will include the term below:

`(-1)^n`

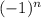
Therefore, the explicit equation for f(n) representing the sequence is:

`f(n)=(-1)^n((n)/(n+4))`

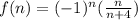
Part C) The sign of f(56) will be:

(-1)^56 = 1

Since this gives us a positive value, the sign of f(56) is positive