Question

An object is dropped from a height of 100m. What height above the ground is the object when it has a speed of 25m/s? (g = 9.8)

Answer 1

Given,

The height from which the object was dropped, h=100 m

The speed of the object, v=25 m/s

The acceleration due to gravity, g=9.8 m/s²

The object will have only potential energy when it is at rest at the height of 100 m. As the object falls it will slowly lose its potential energy. The potential energy thus lost will be converted into the kinetic energy of the object.

Thus the potential energy lost by the object when it has a speed of 25 m/s will be equal to its kinetic energy at that instant.

Therefore,

`\begin{gathered} mg(\Delta h)=(1)/(2)mv^2 \\ \Rightarrow\Delta h=(v^2)/(2g) \end{gathered}`

Where Δh is the change in the height of the object or the height through which the object has fallen at that instant.

On substituting the known values,

`\begin{gathered} \Delta h=(25^2)/(2*9.8) \\ =31.89\text{ m} \end{gathered}`

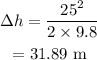
Thus the height of the object above ground is,

`\begin{gathered} l=h-\Delta h \\ =100-31.89 \\ =68.11\text{ m} \end{gathered}`

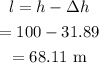
Thus the height of the object above the ground when it has a speed of 25 m/s is 68.11. m