If the number of bacteria in a colony doubles every 72 hours and there is currently a population of 105,700 bacteria, what will the population be 216 hours from now? bacteria

Question

asked Dec 27, 2023 212k views

1 Answer

Pegues · Answer 1 · 2023-12-31T05:10:07+0000

EXPLANATION

Let's see the facts:

Period = 72 hours

Initial Population= 105,700

Time = 216 hours

The equation is as follows:

$P=P_0e^(rt)^{}$

P_0=Initial Population

r= rate of growth

t=time

First, we need to find r:

In 72 hours ------> 2*105,700 = 211,400 bacteria

Replacing terms:

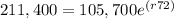
Dividing both sides by 105,700:

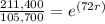
Applying ln to both sides:

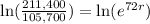
$\ln ((211,400)/(105,700))=\ln (e^(72r))$

Simplifying:

$\ln ((211,400)/(105,700))=72r\cdot\ln e$

Dividing both sides by 72:

$(\ln ((211,400)/(105,700)))/(72)=r$

Switching sides:

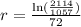
$r=(\ln ((2114)/(1057)))/(72)$

Simplifying:

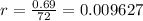
Now that we have r=0.009627 we can calculate the value of P as shown as follows:

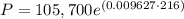
$P=105,700e^((0.009627\cdot216))$

Multiplying terms:

$P=105,700\cdot e^((2.08))^{}$

Now, we can solve the expression:

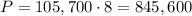
$P=105,700\cdot8=845,600$

The answer is 845,600 bacteria.