EXPLANATION
Let's see the facts:
Period = 72 hours
Initial Population= 105,700
Time = 216 hours
The equation is as follows:
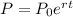
P_0=Initial Population
r= rate of growth
t=time
First, we need to find r:
In 72 hours ------> 2*105,700 = 211,400 bacteria
Replacing terms:
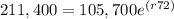
Dividing both sides by 105,700:
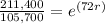
Applying ln to both sides:
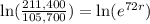
Simplifying:
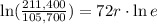
Dividing both sides by 72:
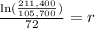
Switching sides:
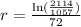
Simplifying:
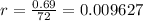
Now that we have r=0.009627 we can calculate the value of P as shown as follows:
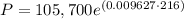
Multiplying terms:
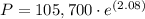
Now, we can solve the expression:
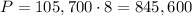
The answer is 845,600 bacteria.