Question

it took Janet one hour longer to travel 75 miles than it did for Bonnie to travel 60 miles Bonnie speed was 5 miles per hour faster than Janet speed. Find Janet speed and Bonnie speed.

Answer 1

Let Janet's speed be x

Bonnie's speed would be 5 + x

The time for Bonnie to travel 60 miles is

`\frac{dis\tan ce}{\text{speed}}=(60)/(5+x)`

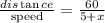
The time for Janet to travel 75 miles is

`(75)/(x)`

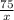
Thus we have from the information

`\begin{gathered} (60)/(5+x)=(75)/(x)-1 \\ (60)/(5+x)=\text{ }(75-x)/(x) \\ \end{gathered}`

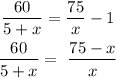
Cross multiply

`\begin{gathered} 60x=(5+x)(75-x) \\ 60x=375-5x-x^2+75x \\ x^2-10x-375=0 \end{gathered}`

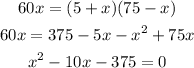
Solving this quadratic equation for x, we have

`\begin{gathered} x^2-25x+15x-375=0 \\ x(x-25)+15(x-25)=0 \\ (x+15)(x-25)=0 \end{gathered}`

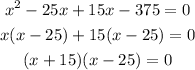
Thus x = -15 or 25.

The speed cannot be a negative number, so x = 25

Therefore Bonnie's speed = 25 miles per hour

and Janet's speed = 25 - 5 = 20 miles per hour