Let Janet's speed be x
Bonnie's speed would be 5 + x
The time for Bonnie to travel 60 miles is
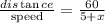
The time for Janet to travel 75 miles is

Thus we have from the information
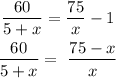
Cross multiply
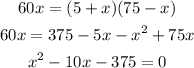
Solving this quadratic equation for x, we have
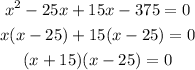
Thus x = -15 or 25.
The speed cannot be a negative number, so x = 25
Therefore Bonnie's speed = 25 miles per hour
and Janet's speed = 25 - 5 = 20 miles per hour