Question

Hi, can you help me to solve this exercise, please!

Answer 1

Given the figure, we can deduce the following information:

1. The measure of angle T is 45°.

2. The leg TS is:

`32\sqrt[]{3}`

To determine SU, we use the formula:

`\sin (\theta)=\frac{opposite}{\text{hypotenuse}}`

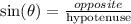
The opposite and hypotenuse sides are shown in the figure below:

We plug in what we know:

`\begin{gathered} \sin (\theta)=\frac{opposite}{\text{hypotenuse}} \\ \sin (45)=\frac{SU}{32\sqrt[]{3}} \\ \text{Simplify and rearrange} \\ SU=\sin (45)(32\sqrt[]{3}) \\ SU=16\sqrt[]{6} \end{gathered}`

Therefore, the answer is:

`\begin{gathered} SU=16\sqrt[]{6} \\ \end{gathered}`