The given function is
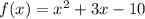
We need to find the solution of
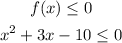
Since the sign of inequality is <=, then the solution will be closed intervales from the small number to the big number [a, b]
At first, factor the left side into 2 factors
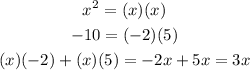
Then the two factors are (x - 2) and (x + 5)
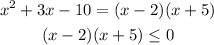
Now, equate each factor by 0 to find the values of x
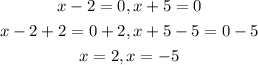
Since the smallest number -s -5 and the greatest number is 2, then
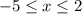
The solution should be a closed interval from -5 to 2
The solution is [-5, 2]
The answer is
A. The solution is [-5, 2]