Question

Circle E has a radius of 4.1 meters. FG is a chord and HE is a perpendicular bisector of FG. If FG = 6.5 meters, calculate the distance of IH.

Answer 1

We have to find the length of IH.

We can draw this as:

Both segments EF and EI are radius of the circle.

Also, EH is the projection of EF into the horizontal axis, and can be written as:

`EH=EF\cdot\cos (\alpha)`

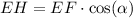
We can also relate FH, that has a length that is half of FG, as the projection of EF in the vertical axis. This can be written as:

`\begin{gathered} FH=(FG)/(2)=EF\cdot\sin (\alpha) \\ (6.5)/(2)=4.1\cdot\sin (\alpha) \\ \sin (\alpha)=(6.5)/(2)\cdot(1)/(4.1)\approx0.79 \\ \alpha=\arcsin (0.79) \\ \alpha\approx52.44\degree \end{gathered}`

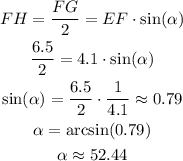
We can use this result to solve for IH as:

`\begin{gathered} IH=EI-EH \\ EI=EF \\ EH=EF\cdot\cos (\alpha) \\ \Rightarrow IH=EF-EF\cdot\cos (\alpha) \\ IH=EF(1-\cos (\alpha)) \\ IH=4.1\cdot(1-\cos (52.44\degree)) \\ IH\approx4.1(1-0.61) \\ IH\approx4.1\cdot0.39 \\ IH\approx1.6 \end{gathered}`

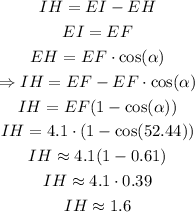
Answer: IH = 1.6 meters