We have to find the length of IH.
We can draw this as:
Both segments EF and EI are radius of the circle.
Also, EH is the projection of EF into the horizontal axis, and can be written as:
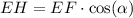
We can also relate FH, that has a length that is half of FG, as the projection of EF in the vertical axis. This can be written as:
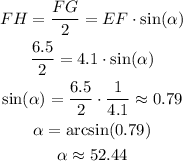
We can use this result to solve for IH as:
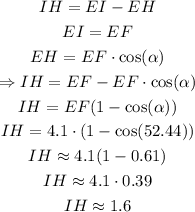
Answer: IH = 1.6 meters