Given:

Required: Derivative of inverse of x at the point x = 1
Explanation:
Use the formula
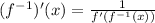
Substitute 1 for x.
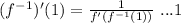
First, find the inverse of f(x).
Let y = f(x). Then y = cos(3x).
Exchange x and y gives x = cos(3y).
Solve for y, which will be the inverse of f(x).
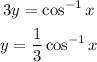
So,
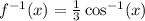
Substitute 1 for x.
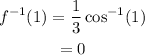
Now, find the derivative of f(x).
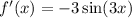
Thus, from equation (1),
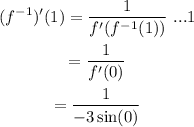
which is not defined. So, the answer not exists.