Question

Use the function f and the given real number a to find (f -1)'(a). (Hint: See Example 5. If an answer does not exist, enter DNE.)f(x) = cos(3x), 0 ≤ x ≤ /3, a = 1

Answer 1

Given:

`f(x)=\cos(3x),0\leq x\leq(\pi)/(3),a=1`

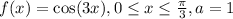
Required: Derivative of inverse of x at the point x = 1

Explanation:

Use the formula

`(f^(-1))^(\prime)(x)=(1)/(f^(\prime)(f^(-1)(x)))`

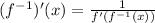
Substitute 1 for x.

`(f^(-1))^(\prime)(1)=(1)/(f^(\prime)(f^(-1)(1)))\text{ ...\lparen1\rparen}`

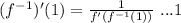
First, find the inverse of f(x).

Let y = f(x). Then y = cos(3x).

Exchange x and y gives x = cos(3y).

Solve for y, which will be the inverse of f(x).

`\begin{gathered} 3y=\cos^(-1)x \\ y=(1)/(3)\cos^(-1)x \end{gathered}`

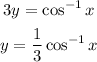
So,

`f^(-1)(x)=(1)/(3)\cos^(-1)(x)`

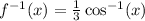
Substitute 1 for x.

`\begin{gathered} f^(-1)(1)=(1)/(3)\cos^(-1)(1) \\ =0 \end{gathered}`

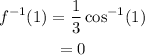
Now, find the derivative of f(x).

`f^(\prime)(x)=-3\sin(3x)`

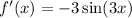
Thus, from equation (1),

`\begin{gathered} (f^(-1))^(\prime)(1)=(1)/(f^(\prime)(f^(-1)(1)))\text{ ...\lparen1\rparen} \\ =(1)/(f^(\prime)(0)) \\ =(1)/(-3\sin(0)) \end{gathered}`

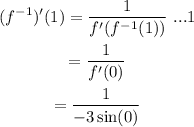
which is not defined. So, the answer not exists.