Question

Find the area of the figure. Dimensions are in inches

Answer 1

We are given a figure and we are asked to determine its area. To do that we need to add the areas of the square and the semi-circle. The area of the square is the measure of its side squared, that is:

`A_s=l^2`

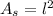
Replacing:

`\begin{gathered} A_{}s=(6in)^2 \\ A_{}s=36in^2 \end{gathered}`

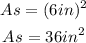
The area of the semi-circle is given by:

`A_(sc)=(\pi r^2)/(2)`

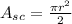
Replacing the value of the radius:

`A_(sc)=(\pi(3in)^2)/(2)`

Solving the operations:

`A_(sc)=14.1in^2`

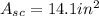
The total area is:

`A=A_s+A_(sc)`

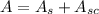
Replacing:

`\begin{gathered} A=36in^2+14.1in^2 \\ A=50.1in^2 \end{gathered}`

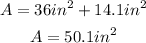
Therefore, the area is 50.1 square inches.