Given:
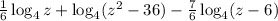
To combine these logarithms into a single logarithm, the first thing we need to do is to re-write the expression as a single logarithm with coeffient.
![(1)/(6)\log _4z+\log _4(z^2-36)-(7)/(6)\log _4(z-6)=\frac{\log _4\sqrt[6]{z}+\log _4(z^2-36)}{\log _4\sqrt[6]{(z-6)^7}}](https://img.qammunity.org/2023/formulas/mathematics/high-school/rpg9rz85m7mpzzxf55j1w9i00y4d2vvk1f.png)
Next, we will use the Product Rule to simplify the numerator.
Product Rule states that:
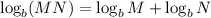
Applying it to the numerator:
![\log _4\sqrt[6]{z}+\log _4(z^2-36)=\log _4(\sqrt[6]{z}(z^2-36))](https://img.qammunity.org/2023/formulas/mathematics/high-school/lxvsghbz83sd4i1yn8f6ktuuljn29anmmu.png)
We will now have a new expression:
![\frac{\log_4(\sqrt[6]{z}(z^2-36))}{\log_4\sqrt[6]{(z-6)^7}}](https://img.qammunity.org/2023/formulas/mathematics/high-school/m0vromg35ozfj0uelmxmhfe43bwi1c7f5o.png)
Next, we will factor out the logarithm.
![\frac{\log_4(\sqrt[6]{z}(z^2-36))}{\log_4\sqrt[6]{(z-6)^7}}=\log _4(\frac{\sqrt[6]{z}(z^2-36)}{\sqrt[6]{(z-6)^7}})](https://img.qammunity.org/2023/formulas/mathematics/high-school/mxn76x13y2awcbi49io3vtpjk77wxb9bpd.png)
Therefore, the final answer would be:
![\log _4(\frac{\sqrt[6]{z}(z^2-36)}{\sqrt[6]{(z-6)^7}})](https://img.qammunity.org/2023/formulas/mathematics/high-school/220rxczqstqglwtmy6pi7ea58xxec1chs1.png)