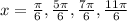We are given the following equation:
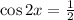
To solve for "x" we will take arccos to both sides:
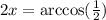
Solving the operations:
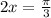
This is for the first quadrant. Dividing both sides by 2:
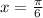
For the second quadrant we have:
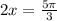
Dividing both sides by 2:
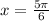
For the third quadrant we have:
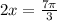
Dividing by 2:
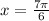
For the fourth quadrant:
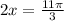
Dividing by 2:
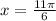
Therefore, the values of "x" are: