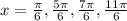Question

Solve for [0,2pi]:cos 2x= 1/2

Answer 1

We are given the following equation:

`\cos 2x=(1)/(2)`

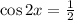
To solve for "x" we will take arccos to both sides:

`2x=\text{arccos}((1)/(2))`

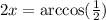
Solving the operations:

`2x=(\pi)/(3)`

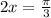
This is for the first quadrant. Dividing both sides by 2:

`x=(\pi)/(6)`

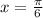
For the second quadrant we have:

`2x=(5\pi)/(3)`

Dividing both sides by 2:

`x=(5\pi)/(6)`

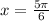
For the third quadrant we have:

`2x=(7\pi)/(3)`

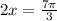
Dividing by 2:

`x=(7\pi)/(6)`

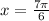
For the fourth quadrant:

`2x=(11\pi)/(3)`

Dividing by 2:

`x=(11\pi)/(6)`

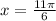
Therefore, the values of "x" are:

`x=(\pi)/(6),(5\pi)/(6),(7\pi)/(6),(11\pi)/(6)`