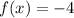ANSWER:
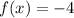
Explanation:
We have that a linear function in its slope and intercepot form is the following:

We calculate the slope as follows:
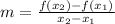
The points to use would be (3, -4) and (5, -4)
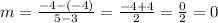
We can see that the slope is 0, which means the function would be: