Question

Find the values X and Y if L ll M .

Answer 1

Let's solve for x first.

To find x, use the interior angles on same side of a transversal theorem.

The interior angles on sam side of a transversal are supplemantary angles, and supplementary angles sum up to 180 degrees.

Thus, we have:

(23x - 16) + (8x - 21) = 180

23x - 16 + 8x - 21 = 180

Combine like terms:

23x + 8x - 21 - 16 = 180

31x - 37 = 180

Add 37 to both sides:

31x - 37 + 37 = 180 + 37

31x = 217

Divide both sides by 31:

`\begin{gathered} (31x)/(31)=(217)/(31) \\ \\ x\text{ = 7} \end{gathered}`

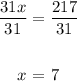
To find y, use the vertical angles theorem.

Vertical angles are congruent.

Thus we have:

7y - 23 = 23x - 16

Since x = 7, substitute x for 7 in the equation above to find y.

7y - 23 = 23(7) - 16

7y - 23 = 161 - 16

7y - 23 = 145

Add 23 to both sides:

7y - 23 + 23 = 145 + 23

7y = 168

Divide both sides by 7:

`\begin{gathered} (7y)/(7)=(168)/(7) \\ \\ y\text{ = }24 \end{gathered}`

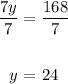
x = 7

y = 24

ANSWER:

x = 7

y = 24