Question

What are the steps I have to do in order to get the solution

Answer 1

we have the expression

`g(x)=(x^2+1)/(f(x))`

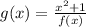
Find out the derivative g'(x)

so

`g^(\prime)(x)=((2x)(f(x)-(x^2+1)\cdot f^(\prime)(x))/((f(x))^2)`

Looking at the graph

f(2)=3

Find out the value of f'(x) at x=2

Find out the slope of f(x) between interval (0,3)

we have the points (0,-5) and (3,7)

m=(7+5)/(3-0)

m=12/3

m=4

so

f'(2)=4

substitute the given values in the expression above

`g^(\prime)(2)=((2\cdot2)(3)-(2^2+1)\cdot4)/((3)^2)`
`g^(\prime)(2)=((4)(3)-(5)\cdot4)/(9)`
`g^(\prime)(2)=-(8)/(9)`

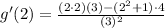
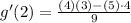
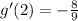
therefore

the answer is option A