Question

To qualify for a police academy, applicants are given a test of physical fitness. The scores are normally distributed with a mean of 65 and a standard deviation of 14. If only the top 20% are selected, find the cutoff score.

Answer 1

mean of 65

standard deviation of 14

top 20% are selected

We need to use the Z-Score table to find the value of Z that represents 80%

In this case, the closest value would be 0.84 as can be seen in the picture below...

Now, we can use this equation...

`Z=(x-\mu)/(\sigma)`

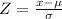
where,

Z=0.84,

x is the cutoff score,

μ is the mean, and

σ is the standard deviation

Now, we replace those values and solve for x, as it follows,

`0.84=(x-65)/(14)`

`\begin{gathered} (x-65)/(14)=0.84 \\ (14\left(x-65\right))/(14)=0.84\cdot\: 14 \\ x-65=11.76 \\ x-65+65=11.76+65 \\ x=76.76 \end{gathered}`

Therefore, the cutoff score is 76.76