STEP - BY - STEP EXPLANATION
What to find?
• Marginal cost as a function of q.
,
• Revenue function in terms of q.
,
• Marginal revenue function in terms of q.
Given:
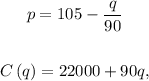
Part A
Marginal cost as a function of q:
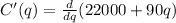
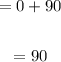
Part B
Revenue function in terms of q.
Revenue = pq
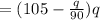
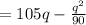
Hence;
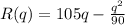
Part C
Marginal revenue function in terms of q.
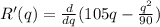
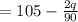
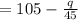
Hence;
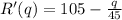
ANSWER
A) C'(q) =90
B) R(q) = 105q - q^2/90
C) R'(q) = 105 - q/45