Question

the first answer choice is 2√6, 3√7, or 6√3the second choice box is 3 and 7, -8.5 and 8.5, or -1 and 1

Answer 1

In order to prove that the diagonals of a square are congruent, first we need to find their length by using the Pythagorean Theorem:

`h^2=a^2+b^2`

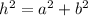
Where h is the hypotenuse of the triangle (in this case the diagonal), a and b are the sides of the triangle. In the coordinate plane, we can see that each side measures 6 units. By replacing these values we can find the length of LN and KM as follows:

`\begin{gathered} \bar{LN}=6^2+6^2 \\ \bar{LN}=36+36 \\ \bar{LN}=72 \\ \bar{LN}=√(72) \\ \bar{LN}=\sqrt[]{36\cdot2} \\ \bar{LN}=\sqrt[]{36}\cdot\sqrt[]{2} \\ \bar{LN}=6\sqrt[]{2} \end{gathered}`

Now, for KM:

`\begin{gathered} \bar{KM}=6^2+6^2 \\ \bar{KM}=36+36 \\ \bar{KM}=72 \\ \bar{KM}=\sqrt[]{36\cdot2} \\ \bar{KM}=\sqrt[]{36}\cdot\sqrt[]{2} \\ \bar{KM}=6\sqrt[]{2} \end{gathered}`

Then, as the diagonals have the same measure they are congruent.

To find the slope, we can use the following formula:

`m=(y2-y1)/(x2-x1)`

Were (x1,y1) and (x2,y2) are the coordinates of two points on the line.

The coordinates of K, L, M and N are:

K(2,1) and M(8,-5)

L(2,-5) and N(8,1).

The slope of KM is:

`m=(-5-1)/(8-2)=(-6)/(6)=-1`

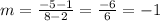
And the slope of LN is:

`m=(1-(-5))/(8-2)=(1+5)/(6)=(6)/(6)=1`

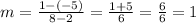
When two lines are perpendicular, the product of their slopes is equal to -1, then if m1