Question

Please help : fill out table first and then explain

Answer 1

R3 and R4 are in series, so:

`R_(eq)1=R3+R4=5+10=15`

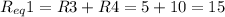
R6 and R7 are also in series, so:

`R_(eq)2=R6+R7=8+7=15`

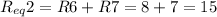
R5, Req1 and Req2 are in parallel, so:

`\begin{gathered} (1)/(R_(eq)3)=(1)/(R_(eq1))+(1)/(R_(eq)2)+(1)/(R5) \\ (1)/(R_(eq)3)=(1)/(15)+(1)/(15)+(1)/(15) \\ (1)/(R_(eq)3)=(3)/(15) \\ (1)/(R_(eq)3)=(1)/(5) \\ R_(eq)3=5 \end{gathered}`

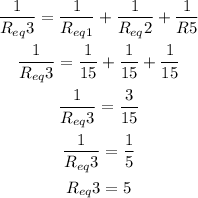
Now, Req 3, R10 and R11 are in series, so:

`R_(eq)4=R_(eq)3+R10+R11=5+10+15=30`

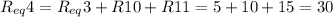
Now, we can find the total current in that segment using ohm law:

`\begin{gathered} V=IR \\ I=(V)/(R) \\ I1=(V_T)/(R_(eq)4)=(240)/(30) \\ I1=8A \end{gathered}`

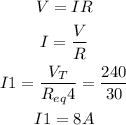
Now, let's find the voltage and the current for R3,R4, R5, R6, R7, R10 and R11

`\begin{gathered} V1=I1\cdot R_(eq)3=8\cdot5=40V \\ \end{gathered}`

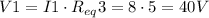
With this value, let's complete one portion of the table:

---------------

Now, R8 and R9 are in series, so:

`R_(eq)5=R8+R9=20+40=60`

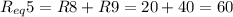
Req5 and Req4 are in parallel, so:

`\begin{gathered} (1)/(R_(eq)6)=(1)/(R_(eq)4)+(1)/(R_(eq)5) \\ (1)/(R_(eq)6)=(1)/(30)+(1)/(60) \\ (1)/(R_(eq)6)=(1)/(20) \\ R_(eq)6=(20)/(1) \\ R_(eq)6=20 \end{gathered}`

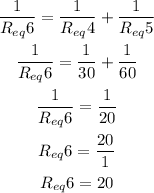
R1 and R2 are in parallel, R12 and R13 are in parallel too, so:

`\begin{gathered} (1)/(R_(eq)7)=(1)/(R1)+(1)/(R2) \\ (1)/(R_(eq)7)=(1)/(10)+(1)/(10) \\ (1)/(R_(eq)7)=(2)/(10) \\ R_(eq)7=5 \end{gathered}`
`\begin{gathered} (1)/(R_(eq)8)=(1)/(R12)+(1)/(R13) \\ (1)/(R_(eq)8)=(1)/(12)+(1)/(60) \\ (1)/(R_(eq)8)=(1)/(10) \\ R_(eq)8=10 \end{gathered}`

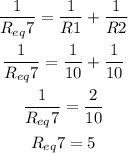
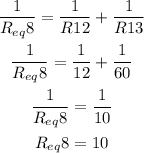
Therefore, the total resistance of the circuit since Req6, Req 7, Req8 and R14 are in series, is:

`\begin{gathered} R_T=R_(eq)6+R_(eq)7+R_(eq)8+R14=20+5+10+5 \\ R_T=40 \end{gathered}`

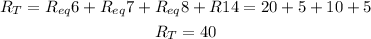
And the total current is:

`I_T=(V_T)/(R_T)=(240)/(40)=6_{}`

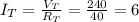
Answer: