Question

2 = logae. I need help please

Answer 1

Hello there. To solve this question, we'll have to remember some properties about logarithms.

Given the logarithmic equation:

`2=\log _ae`

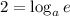
We have to determine the base a.

For this, remember that the logarithmic function is defined as

`\log _ab`

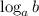
For values of a, b such that

`\begin{gathered} 00 \end{gathered}`

Also, we need the following property:

`\log _ab=c\leftrightarrows b=a^c`

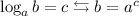
Such that we have:

`\begin{gathered} 2=\log _ae \\ \Rightarrow e=a^2 \end{gathered}`

Take the square root on both sides of the equation

`\begin{gathered} \sqrt[]{e}=\sqrt[]{a^2} \\ |a|=\sqrt[]{e} \end{gathered}`

This gives us two solutions, according to the definition of the absolute value function:

`|x|=\begin{cases}x,\text{ if x is greater than or equal to zero} \\ -x,\text{ if x is less than zero}\end{cases}`

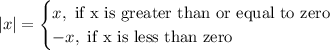
In this case, remember that a > 0, so the only solution we're interested is:

`a=\sqrt[]{e}`

In this case, we've showed that:

`\log _{\sqrt[]{e}}e=2`

In fact, all the other properties hold and this is the solution for the base a in this logarithmic equation.