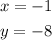Question

8x+y=-16-3x+y=-5elimination

Answer 1

To solve the system of equations

`\begin{gathered} 8x+y=-16 \\ -3x+y=-5 \end{gathered}`

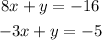
By elimination, the firts thing to do is to make sure that the coefficients of one of the variables are the same in both equations. In this case, we note that the coefficients of y in both equations are 1.

Once we have that, we are going to substract the equations.

Then

`\begin{gathered} 8x+y=-16 \\ -(-3x+y)=-(-5) \\ --------------------- \\ 8x+y=-16 \\ 3x-y=5 \\ ---------------------- \\ \text{Then we add },\text{ so that we have} \\ 11x=-11 \end{gathered}`

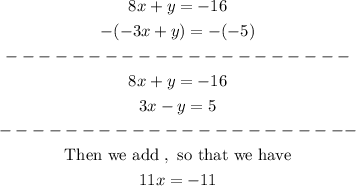
Once we elimate one of the variables we solve the remaining equation

`\begin{gathered} 11x=-11 \\ x=-(11)/(11) \\ x=-1 \end{gathered}`

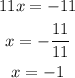
To eliminate the variable x, we have to multiply each equations by an appropiate number so that both coefficients are the same in both equations. In this case we are going to multiply the first equation by 3 and the second by 8

`\begin{gathered} (8x+y=-16)(3) \\ (-3x+y=-5)(8) \\ \text{Then } \\ 24x+3y=-48 \\ -24x+8y=-40 \end{gathered}`

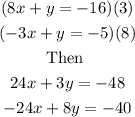
Note that both coefficients of x are the same, then we add the equations.

`\begin{gathered} 24x+3y=-48 \\ -24x+8y=-40 \\ ---------------- \\ 11y=-88 \end{gathered}`

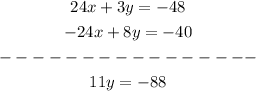
Then we solve for y

`\begin{gathered} 11y=-88 \\ y=-(88)/(11) \\ y=-8 \end{gathered}`

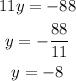
Then the answer for this system is

`\begin{gathered} x=-1 \\ y=-8 \end{gathered}`