Given:
The growth of the herd will be modelled by the equation.
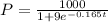
Where P = Population of the herd
t = time in months
Required:
To find the population after t months.
Step-by-step explanation:
Substitute t= 5 in the given equation.
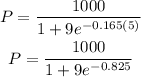
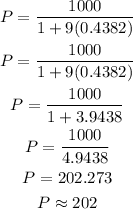
Final Answer:
The population after 5 months is 202 animals expected.