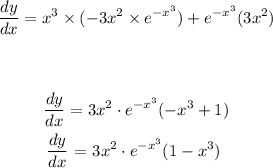Answer:

Step-by-step explanation:
Here, we want to find the derivative of the given function
To do this, we are going to use the product rule
Mathematically, we have the product rule as follows:
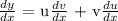
where:
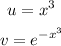
We proceed as follows to find the unit derivatives:
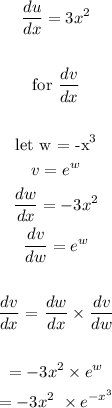
We put together the final answer as follows: