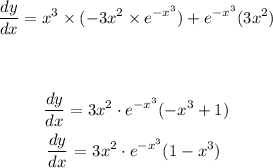Question

Can you answer this question.Find the derivative of the given function

Answer 1

`(dy)/(dx)\text{ = }3x^2\cdot e^(-x^3)(1-x^3)\text{ }`

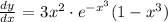
Step-by-step explanation:

Here, we want to find the derivative of the given function

To do this, we are going to use the product rule

Mathematically, we have the product rule as follows:

`(dy)/(dx)\text{ = u}(dv)/(dx)\text{ + v}(du)/(dx)`

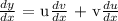
where:

`\begin{gathered} u=x^3 \\ v=e^(-x^3) \end{gathered}`

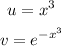
We proceed as follows to find the unit derivatives:

`\begin{gathered} (du)/(dx)=3x^2 \\ \\ \text{for }(dv)/(dx) \\ \\ \text{let w = -x}^3 \\ v=e^w \\ (dw)/(dx)=-3x^2 \\ (dv)/(dw)=e^w \\ \\ (dv)/(dx)\text{ = }(dw)/(dx)*(dv)/(dw) \\ \\ =-3x^2* e^w \\ =-3x^2\text{ }* e^(-x^3) \end{gathered}`

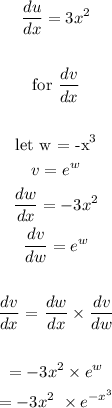
We put together the final answer as follows:

`\begin{gathered} (dy)/(dx)=x^3*(-3x^2* e^(-x^3))+e^(-x^3)(3x^2) \\ \\ \\ (dy)/(dx)=3x^2\cdot e^(-x^3)(-x^3+1) \\ (dy)/(dx)\text{ = }3x^2\cdot e^(-x^3)(1-x^3)\text{ } \end{gathered}`