Using this drawing as a guide, the problem becomes easier to tackle. In every triangle, the sum of all 3 angles must be equal to 180 degrees. You have no way of knowing the angle that would be B, so a good strategy is to cut a line just below the angle C so you get 2 right triangles.
Then, using the sine law, you can use that sin(A)=a'/b, where a' is not a but the right side of the new triangle.
By using the previous formula, you get that b*sin(A)=a'=50*sin(60 degrees)=43.3. You also have that cos(A)=(c-x)/b so -cos(A)*b +c=x
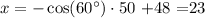
So, with a' and x, you can apply the Pythagorean theorem to find a.
![a^(\prime2)+x^2=a^2\rightarrow a=\sqrt[]{23^2+43.3^2}=49.0](https://img.qammunity.org/2023/formulas/mathematics/college/jbemtgwtb2fw7qnq9dy4f7tmzyfrt48gsq.png)
This is the length a, which is the final answer.