Solving the We are asked to determine the number of permutation of 4 students taken from a set of 15.
The total number of permutations of "k" objects taken from a set of "n" elements is given by:
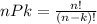
Where:

the value of "n!" is given by:

From the given problem we have:
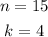
Substituting the values we get:

Solving the operations:
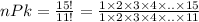
Solving the products:
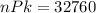
Therefore, there are 32760 permutations.