Question

We often deal with weighted means, in which different data values carry different weights in the calculation of the mean. For example, if the final exam counts for 50% of your final grade and 2 midterms each count for 25%, then you must assign weights of 50% and 25% to the final and midterms, respectively, before computing the mean score for the term. Apply the idea of weighted mean in the following exercise.A student is taking an advanced antonomy class in which the midterm and final exams are worth 40% each and homework is worth 20% of his final grade. On a 100-point scale, his midterm exam score was 84.1 , his homework average score was 96.8 , and his final exam score was 86.6 . Complete parts (a) and (b) below.Question content area bottomPart 1a. On a 100-point scale, what is the student's overall average for the class?His overall average is?

Answer 1

`87.6`

Step-by-step explanation:

Here, we want to get his overall average

From the given question:

The midterm and final exams are worth 40% each and homework is worth 20%

His score for the midterm exam is 84.1/100 (worth 40%), his final exam score is 86.6/100 (40%) while the average homework score is worth 96.8/100 (20%)

We have the overall average calculated as follows:

`\begin{gathered} 0.4(84.1)\text{ + 0.4\lparen86.6\rparen + 0.2\lparen96.8\rparen} \\ =\text{ 87.64} \end{gathered}`

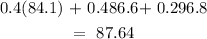
To the nearest tenth, we have this as 87.6